В прошлый раз мы познакомились с различными активационными функциями, научились выбирать подходящую функцию для своего проекта и создали слои активации для нескольких функций. Сегодня мы рассмотрим работу полносвязного слоя, научимся считать градиенты для обратного распространения ошибки и обновлять весовые коэффициенты с помощью градиентного спуска, а также опишем класс для этого слоя.
Что такое полносвязный слой
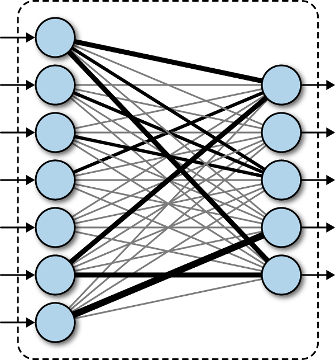
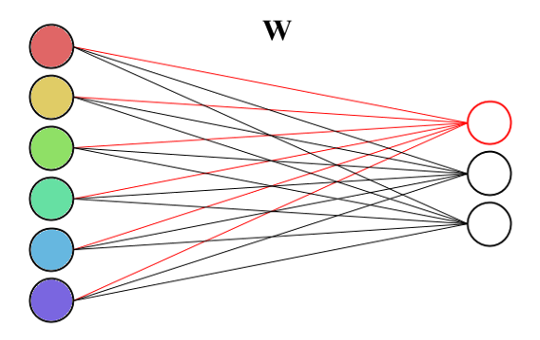
Полносвязный слой — слой, выходные нейроны которого связаны со всеми входными нейронами. Нейроном в данном случае называется математическая модель искуственного нейрона, основанная на представлении о биологическом нейроне, однако в действительности не имеющая с ним практически ничего общего. Будем называть нейроном взвешенную сумму значений входного вектора x, к которой затем применяется функция активации σ(y): z = σ(y), y = w0 + w1·x1 + w2·x2 + ... + wn·xm. В полносвязном слое находится N таких нейронов, поэтому выходом слоя является не одно число, а целый вектор z: zi = σ(wi0 + wi1·x1 + wi2·x2 + ... + wim·xm). Подробнее про искуственный нейрон вы можете посмотреть в нашей статье о создании сети прямого распространения.
Связь с матрицами
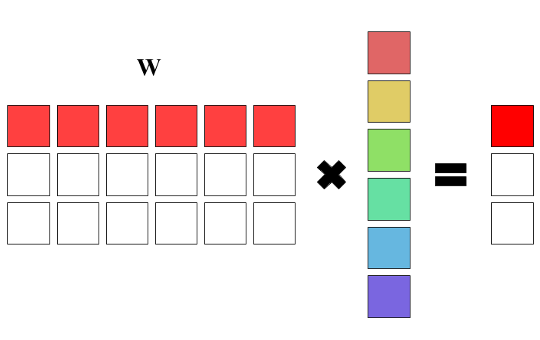
Так как в полносвязном слое обычно находится больше одного нейрона, то нужно найти способ хранения весовых коэффициентов этих нейронов. Самым простым решением будет создание вектора нейронов, однако если присмотреться, то несложно заметить, что для хранения весов нейронов можно использовать обычную матрицу, а для получения выходного вектора просто умножать входной вектор на неё. Действительно, умножение вектора на матрицу даёт n взвешенных сумм, где весовыми коэффициентами являются строки матрицы весов: y = W·x + b. Это весьма удобный способ хранения, так как умножение матрицы на вектор весьма эффективно реализуется в библиотеках линейной алгебры. Но поскольку нашей целью является написание сети с нуля, то мы не будем использовать никаких сторонних библиотек для этого, а напишем всё самостоятельно.
Зачем нужен полносвязный слой
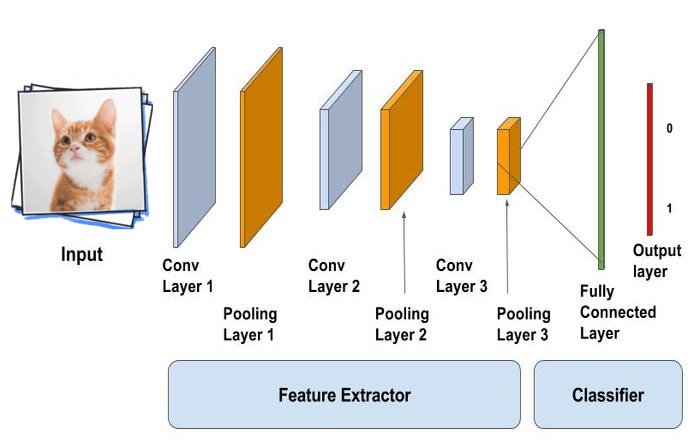
Основной задачей полносвязного слоя является моделирование сложной нелинейной функции, чаще всего используемой для классификации. Эта функция оптимизируется в процессе обучения сети, что позволяет улучшать качество распознавания. Можно считать, что слои, идущие до полносвязного, являются средствами предобработки изображения, а дальнейшая классификация выполняется обычной сетью прямого распространения. То есть всё, что идёт до полносвязного слоя, используется для выделения различных признаков, которые затем подаются на вход классификатору.
Класс матрица
Выше мы выяснили, что полносвязный слой содержит матрицу весовых коэффициентов. В качестве матрицы можно было бы использовать тензор с глубиной равной 1, но для большей наглядности мы создадим отдельный класс для неё. В классе будет два числа — число строк и число столбцов матрицы, а также вектор векторов для хранения самих значений. Для получения и изменения элементов матрицы понадобится индексация — перегрузим для этого оператор круглые скобки:
class Matrix {
int rows; // число строк
int columns; // число столбцов
std::vector<std::vector<double>> values; // значения
public:
Matrix(int rows, int columns); // конструктор из заданных размеров
double& operator()(int i, int j); // индексация
double operator()(int i, int j) const; // индексация
};
В конструкторе сохраним переданные размеры и создадим векторы с заданным числом элементов:
// конструктор из заданных размеров
Matrix::Matrix(int rows, int columns) {
this->rows = rows; // сохраняем число строк
this->columns = columns; // сохраняем число столбцов
values = std::vector<std::vector<double>>(rows, std::vector<double>(columns, 0)); // создаём векторы для значений матрицы
}
Перегрузим оператор круглые скобки для индексации:
// индексация
double& Matrix::operator()(int i, int j) {
return values[i][j];
}
// индексация
double Matrix::operator()(int i, int j) const {
return values[i][j];
}
Создадим класс для слоя
В классе нам потребуется хранить матрицу весовых коэффициентов и вектор весов смещений. Поскольку слой содержит обучаемые параметры, их нужно будет инициализировать, так что добавим генератор случайных чисел с нормальным распределением.
Помимо этого нужно добавить возможность применения активационной функции, а потому потребуется знать, какую функцию активации применять. Для этого создадим перечисление из основных функций активации и при создании слоя будем передавать имя активационной функции через строковый параметр. Для обратного распространения ошибки, как известно из предыдущей статьи, необходимо будет вычислять производные активационных функций, а потому добавим тензор df, который будет хранить эти значения. Для применения функции активации напишем метод Activate, который также будет заполнять значения производной выбранной функции.
class FullyConnectedLayer {
// тип активационной функции
enum class ActivationType {
None, // без активации
Sigmoid, // сигмоидальная функция
Tanh, // гиперболический тангенс
ReLU, // выпрямитель
LeakyReLU, // выпрямитель с утечкой
ELU // экспоненциальный выпрямитель
};
TensorSize inputSize; // входой размер
TensorSize outputSize; // выходной размер
std::default_random_engine generator;
std::normal_distribution<double> distribution;
int inputs; // число входных нейронов
int outputs; // число выходных нейронов
ActivationType activationType; // тип активационной функции
Tensor df; // тензор производных функции активации
Matrix W; // матрица весовых коэффициентов
Matrix dW; // матрица градиентов весовых коэффициентов
std::vector<double> b; // смещения
std::vector<double> db; // градиенты смещений
ActivationType GetActivationType(const std::string& activationType) const; // получение типа активационной функции по строке
void InitWeights(); // инициализация весовых коэффициентов
void Activate(Tensor &output); // применение активационной функции
public:
FullyConnectedLayer(TensorSize size, int outputs, const std::string& activationType = "none"); // создание слоя
Tensor Forward(const Tensor &X); // прямое распространение
Tensor Backward(const Tensor &dout, const Tensor &X); // обратное распространение
void UpdateWeights(double learningRate); // обновление весовых коэффициентов
};
Создание слоя
Слой создаётся из размера входного тензора, количества выходный нейронов и типа функции активации. Внутри конструктора слоя необходимо запомнить входной и выходной размеры, получить тип активационной функции, а также проинициализировать весовые коэффициенты.
FullyConnectedLayer::FullyConnectedLayer(TensorSize size, int outputs, const std::string& activationType) : W(outputs, size.height * size.width * size.deep), dW(outputs, size.height * size.width * size.deep), df(1, 1, outputs), distribution(0.0, sqrt(2.0 / (size.height * size.width * size.deep))) {
// запоминаем входной размер
inputSize.width = size.width;
inputSize.height = size.height;
inputSize.depth = size.depth;
// вычисляем выходной размер
outputSize.width = 1;
outputSize.height = 1;
outputSize.depth = outputs;
this->inputs = size.height * size.width * size.deep; // запоминаем число входных нейронов
this->outputs = outputs; // запоминаем число выходных нейронов
this->activationType = GetActivationType(activationType); // получаем активационную функцию
b = std::vector<double>(outputs); // создаём вектор смещений
db = std::vector<double>(outputs); // создаём вектор градиентов по весам смещения
InitWeights(); // инициализируем весовые коэффициенты
}
Получение типа активационной функции
Так как мы решили (почему-то) передавать тип функции активации в виде строки, а внутри класса работаем со значением перечисления ActivationType, нам необходимо описать метод, получающий значение перечисления по введённой строке. В нём также нужно будет проверить, что введённая строка действительно описывает одну из функций активации, а не какой-нибудь мусор. Для этого мы будем бросать исключение, если ни одна из ожидаемых функций активации не подошла:
// получение типа активационной функции по строке
FullyConnectedLayer::ActivationType FullyConnectedLayer::GetActivationType(const std::string& activationType) const {
if (activationType == "sigmoid")
return ActivationType::Sigmoid;
if (activationType == "tanh")
return ActivationType::Tanh;
if (activationType == "relu")
return ActivationType::ReLU;
if (activationType == "leakyrelu")
return ActivationType::LeakyReLU;
if (activationType == "elu")
return ActivationType::ELU;
if (activationType == "none" || activationType == "")
return ActivationType::None;
throw std::runtime_error("Invalid activation function");
}
Инициализация весовых коэффициентов
Для инициализации обучаемых параметров нужно пройтись по всем значениям матрицы коэффициентов и задать им случайные значения. Исключение составляют веса смещения — им мы зададим значения 0.01:
// инициализация весовых коэффициентов
void FullyConnectedLayer::InitWeights() {
for (int i = 0; i < outputs; i++) {
for (int j = 0; j < inputs; j++)
W(i, j) = distribution(generator); // генерируем очередное случайное число
b[i] = 0.01; // все смещения делаем равными 0.01
}
}
Прямое распространение
В прямом распространении нужно умножить матрицу весовых коэффициентов на входной тензор, представленный в виде одномерного вектора, прибавить вес смещения, а затем применить активационную функцию. Мы начнём с написания метода, который помимо применения активационной функции, будет вычислять ещё и значение её производной:
// применение активационной функции с вычислением значений её производной
void FullyConnectedLayer::Activate(Tensor &output) {
if (activationType == ActivationType::None) {
for (int i = 0; i < outputs; i++) {
df[i] = 1;
}
}
else if (activationType == ActivationType::Sigmoid) {
for (int i = 0; i < outputs; i++) {
output[i] = 1 / (1 + exp(-output[i]));
df[i] = output[i] * (1 - output[i]);
}
}
else if (activationType == ActivationType::Tanh) {
for (int i = 0; i < outputs; i++) {
output[i] = tanh(output[i]);
df[i] = 1 - output[i] * output[i];
}
}
else if (activationType == ActivationType::ReLU) {
for (int i = 0; i < outputs; i++) {
if (output[i] > 0) {
df[i] = 1;
}
else {
output[i] = 0;
df[i] = 0;
}
}
}
else if (activationType == ActivationType::LeakyReLU) {
for (int i = 0; i < outputs; i++) {
if (output[i] > 0) {
df[i] = 1;
}
else {
output[i] *= 0.01;
df[i] = 0.01;
}
}
}
else if (activationType == ActivationType::ELU) {
for (int i = 0; i < outputs; i++) {
if (value > 0) {
df[i] = 1;
}
else {
output[i] = exp(output[i]) - 1;
df[i] = output[i] + 1;
}
}
}
}
Теперь напишем прямое распространение. Чтобы умножить матрицу на входной вектор, нужно в каждой строке матрицы пройись по всем её элементам и умножить их на соответствующие элементы входного вектора Х. Для получения выходного значения к получаемому в каждой строке числу нужно прибавить вес смещения и записать в выходной тензор результат активационной функции. В целях оптимизации мы будем сначала записывать значения произведения матрицы на вектор с добавленным весом смещения, а уже затем проходиться по всем полученным значениям и применять активационную функцию:
// прямое распространение
void FullyConnectedLayer::Forward(const Tensor &X) {
Tensor output(outputSize); // создаём выходной тензор
// проходимся по каждому выходному нейрону
for (int i = 0; i < outputs; i++) {
double sum = b[i]; // прибавляем смещение
// умножаем входной тензор на матрицу
for (int j = 0; j < inputs; j++)
sum += W(i, j) * X[j];
output[i] = sum;
}
Activate(output); // применяем активационную функцию
return output; // возвращаем выходной тензор
}
Обратное распространение ошибки
Обратное распространеине ошибки для полносвязного слоя можно разделить на два этапа: вычисление градиентов по весовым коэфициентам, которое делится на вычисление градиентов смещений и градиентов матрицы, и вычисление градиентов по входам:
- Градиентами по весам смещения являются произведения градиентов следующего слоя на значение производной функции активации:
db = dout*df - Для вычисления градиентов матрицы весов нужно умножить градиенты следующего слоя и значения производной активационной функции на входные значения:
dW = (dout*df)·X - Для вычисления градиентов по входам нужно умножить градиенты следующего слоя и значения производной активационной функции на транспонированную матрицу весовых коэффициентов:
dX = WT·(dout*df)
Поскольку постоянно перемножать выходные градиенты на производные не очень эффективно, перед вычислением градиентов домножим тензор производных на тензор градиентов следующего слоя. В результате получится следующий метод для выполнения обратного распространения:
// обратное распространение
Tensor FullyConnectedLayer::Backward(const Tensor &dout, const Tensor &X) {
// домножаем производные на градиенты следующего слоя для сокращения количества умножений
for (int i = 0; i < outputs; i++)
df[i] *= dout[i];
// вычисляем градиенты по весовым коэффициентам
for (int i = 0; i < outputs; i++) {
for (int j = 0; j < inputs; j++)
dW(i, j) = df[i] * X[j];
db[i] = df[i];
}
Tensor dX(inputSize); // создаём тензор для градиентов по входам
// вычисляем градиенты по входам
for (int j = 0; j < inputs; j++) {
double sum = 0;
for (int i = 0; i < outputs; i++)
sum += W(i, j) * df[i];
dX[j] = sum; // записываем результат в тензор градиентов
}
return dX; // возвращаем тензор градиентов
}
Обновление весовых коэффициентов
Обновление весовых коэффициентов полносвязного слоя ничем не отличается от обновления параметров свёрточного слоя: из каждого весового коэффициента нужно вычесть значение градиента, умноженное на скорость обучения:
// обновление весовых коэффициентов
void FullyConnectedLayer::UpdateWeights(double learningRate) {
for (int i = 0; i < outputs; i++) {
for (int j = 0; j < inputs; j++)
W(i, j) -= learningRate * dW(i, j);
b[i] -= learningRate * db[i]; // обновляем веса смещения
}
}
Тестирование
Чтобы убедиться, что слой создан корректно, мы проверим его работу с определёнными весами. Сейчас у нас нет возможности задать определённые весовые коэффициенты слою, поэтому добавим два метода для установки весов матрицы и весов смещения:
// установка веса матрицы
void FullyConnectedLayer::SetWeight(int i, int j, double weight) {
W(i, j) = weight;
}
// установка веса смешения
void FullyConnectedLayer::SetBias(int i, double bias) {
b[i] = bias;
}
Теперь же, имея возможность задать свои собственные веса слою проверим работу прямого и обратного распространения. Для этого, аналогично свёрточному слою, мы написали тестирующую функцию, но ввиду её тривиальности приведём лишь данные для тестирования и ожидаемые результаты. Для проверки создадим полносвязный слой, принимающий на входе тензор размером 1х1х8, и состоящий из 4 нейронов и использующий активационную функцию ReLU. Таким образом размер выходного тензора будет 1х1х4:
| 1 2 3 4 -1 -2 -3 -4 | W: | 1 0 0 1 -1 2 -3 4 | | 1 1 1 1 -3 -4 -5 -6 | | 1 2 2 1 2 2 -3 -8 | b: | 0 0 0 0 | X: | 1 2 -3 4 0 -7 2 -4 |
Если всё сделано правильно, то на выходе должен получиться следующий тензор:
Y: | 36 0 46 15 |
Для обратного распространения зададим следующие градиенты:
dout: | -0.5 0.1 -0.25 0.7 |
Выполнив обратное распространение ошибки слой должен вернуть такой тензор:
dX: | -0.05 0.15 -0.35 -1.55 2.65 3.4 0.65 -2.1 |
Итоги
Мы познакомились с ещё одним слоем свёрточной нейронной сети. И хотя этот слой не самый главный в сети, он всё равно занимает второе место по значимости. На текущий момент у нас в распоряжении находятся уже 4 типа слоёв, которые позволяют перейти к самой главной части — созданию и обучению нашей собственной свёрточной сети.