Нейросети кажутся людям чем-то очень сложным и запутанным, однако это вовсе не так. Простую нейросеть можно написать менее чем за час с нуля. В нашей статье мы создадим нейронную сеть прямого распространения (также называемую многослойным перцептроном), используя лишь массивы, циклы и условные операторы, а значит этот код легко можно будет перенести на любой язык программирования, предоставляющий эти возможности. А если язык предоставляет библиотеку для матричных и векторных вычислений (как, например, numpy в языке Python, то написание займёт ещё меньше времени).
Что такое нейросеть?
Согласно Википедии, искусственная нейронная сеть (ИНС) — математическая модель, а также её программное или аппаратное воплощение, построенная по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма.
Более простыми словами, это некий чёрный ящик, который превращает входные данные в выходные, или, говоря более математическим языком, является отображением пространства входных признаков X в пространство выходных признаков Y: X → Y. То есть мы хотим найти какую-то функцию F, которая сможет выполнять это преобразование. Для начала этой информации нам будет достаточно. Для более подробного ознакомления рекомендуем ознакомиться с этой статьёй на хабре.
Коротко об искусственном нейроне
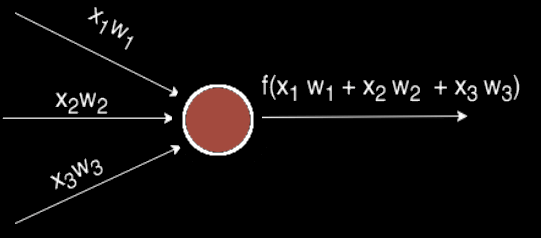
Чаще всего в подобных статьях начинают расписывать про устройство биологического нейрона, связь с его искусственной моделью и прочую лирику. Мы же этого делать не будем, а сразу перейдём к сути. Искусственный нейрон — это всего лишь взвешенная сумма значений входного вектора элементов, которая передаётся на нелинейную функцию активации f: z = f(y), где y = w0·x0 + w1·x1 + ... + wm - 1·xm - 1. Здесь w0, ..., wm - 1 — коэффициенты, веса каждого элемента вектора, x0, ..., xm - 1 — значения входного вектора X, y — взвешенная сумма элементов X, а z — результат применения функции активации. Мы вернёмся к функции активации немного позднее, а пока давайте придумаем, как вместо одного выходного значения получить n.
Нейронный слой
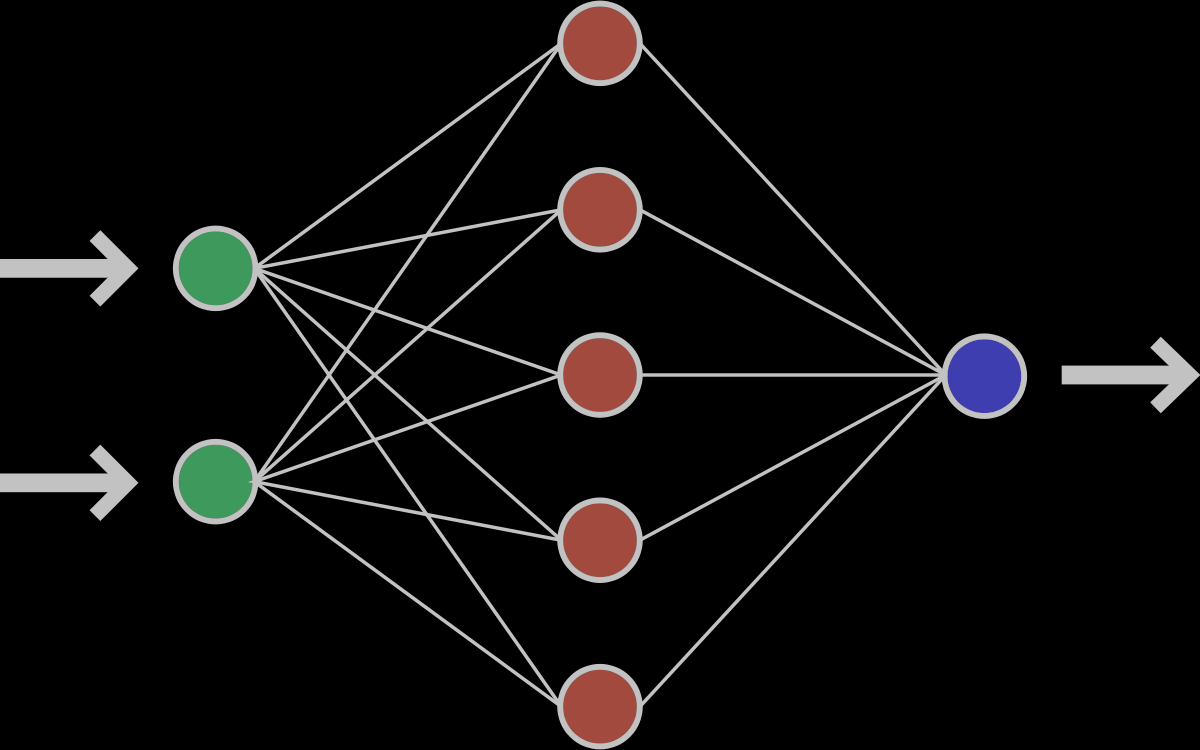
Один нейрон способен входной вектор превратить в одну точку, однако по условию мы хотим получить несколько точек, так как выходной вектор Y может иметь произвольную размерность, определяемую лишь конкретной ситуацией (один выход для XOR, 10 выходов для определения принадлежности к одному из 10 классов и т.д.). Как же нам получить n точек, преобразуя элементы входного вектора X? Оказывается, всё довольно просто: для того, чтобы получить n выходных значений, необходимо использовать не один нейрон, а n. Тогда для каждого из элементов выходного вектора Y будет использовано ровно n различных взвешенных сумм от вектора X. То есть мы получаем, что zi = f(yi) = f(wi0·x0 + wi1·x1 + ... + wim - 1·xm - 1)
Если внимательно посмотреть, то оказывается, что написанная выше формула является определением умножения матрицы на вектор. И действительно, если взять матрицу W размера n на m и умножить её на вектор X размерности m, то получится другой вектор размерности n, то есть ровно то, что нам и нужно. Таким образом, получение выходного вектора по входному для n нейронов можно записать в более удобной матричной форме: Y = W·X, где W — матрица весовых коэффициентов, X — входной вектор и Y — выходной вектор. Однако полученный вектор является неактивированным состоянием (промежуточным, невыходным) всех нейронов, а чтобы получить выходное значение,, необходимо каждое неактивированное значение подать на вход функции активации. Результат её применения и будет выходным значением слоя.
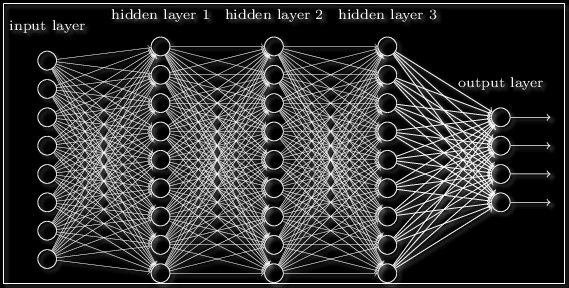
Забегая вперёд скажем о том, что нередко используют последовательность нейронных слоёв для более глубокого обучения сети и большей формализации данных. Поэтому для получения итогового выходного вектора необходимо проделать описанную выше операцию несколько раз подряд от одного слоя к другому. Тогда для первого слоя входным вектором будет X, а для всех последующих входом будет являться выход предыдущего слоя. К примеру, сеть с 3 скрытыми слоями может выглядеть так:
Функция активации
Функция активации — это функция, которая добавляет в сеть нелинейность, благодаря чему нейроны могут довольно точно имитировать любую функцию. Наиболее распространёнными функциями активации являются:
- Сигмоида:
f(x) = 1 / (1 + e-x) - Гиперболический тангенс:
f(x) = tanh(x) - ReLU:
f(x) = max(x,0)
У каждой из них есть свои особенности, но об этом лучше почитать в другой статье.
Хватит бла бла, давайте писать код
Теперь нам достаточно знаний, чтобы написать код получения результата нейронной сети. Мы будем писать код на языке C#, однако, уверяем, код будет практически идентичным для других языков программирования. Давайте разберёмся, что нам потребуется для реализации сети прямого распространения:
- Вектор (входные, выходные);
- Матрица (каждый слой содержит матрицу весовых коэффициентов);
- Нейросеть.
1. Вектор:
- Вектор можно создавать из количества элементов (длины);
- Вектор можно создавать из перечисления вещественных чисел;
- Можно получать значения по индексу i.
- Можно изменять значения по индексу i.
Напишем же это:
class Vector {
public double[] v; // значения вектора
public int n; // длина вектора
// конструктор из длины
public Vector(int n) {
this.n = n; // копируем длину
v = new double[n]; // создаём массив
}
// создание вектора из вещественных значений
public Vector(params double[] values) {
n = values.Length;
v = new double[n];
for (int i = 0; i < n; i++)
v[i] = values[i];
}
// обращение по индексу
public double this[int i] {
get { return v[i]; } // получение значение
set { v[i] = value; } // изменение значения
}
}
2. Матрица:
- Матрицу можно создавать из числа строк, столбцов и генератора случайных чисел для заполнения случайными значениями;
- Можно получать значения по индексам i и j;
- Можно изменять значения по индексам i и j;
Напишем же это:
class Matrix {
double[][] v; // значения матрицы
public int n, m; // количество строк и столбцов
// создание матрицы заданного размера и заполнение случайными числами из интервала (-0.5, 0.5)
public Matrix(int n, int m, Random random) {
this.n = n;
this.m = m;
v = new double[n][];
for (int i = 0; i < n; i++) {
v[i] = new double[m];
for (int j = 0; j < m; j++)
v[i][j] = random.NextDouble() - 0.5; // заполняем случайными числами
}
}
// обращение по индексу
public double this[int i, int j] {
get { return v[i][j]; } // получение значения
set { v[i][j] = value; } // изменение значения
}
}
3. Сама нейросеть:
class Network {
Matrix[] weights; // матрицы весов слоя
int layersN; // число слоёв
// создание сети из массива количества нейронов в каждом слое
public Network(int[] sizes) {
Random random = new Random(DateTime.Now.Millisecond); // создаём генератор случайных чисел
layersN = sizes.Length - 1; // запоминаем число слоёв
weights = new Matrix[layersN]; // создаём массив матриц
// для каждого слоя создаём матрицы весовых коэффициентов
for (int k = 1; k < sizes.Length; k++) {
weights[k - 1] = new Matrix(sizes[k], sizes[k - 1], random);
}
}
// получение выхода сети (прямое распространение)
Vector Forward(Vector input) {
Vector output; // будущий выходной вектор
for (int k = 0; k < layersN; k++) {
output = new Vector(weights[k].n); // создаём новый выходной вектор для каждого слоя
for (int i = 0; i < weights[k].n; i++) {
double y = 0; // неактивированный выход нейрона
for (int j = 0; j < weights[k].m; j++)
y += weights[k][i, j] * input[j];
// выполняем активацию с помощью сигмоидальной функции
output[i] = 1 / (1 + Math.Exp(-y));
// выполняем активацию с помощью гиперболического тангенса
// output[i] = Math.Tanh(y);
// выполняем активацию с помощью ReLU
// output[i] = Math.Max(0, y);
}
}
return output;
}
}
Сеть есть, но её ответы случайны. Как обучать?
На данный момент мы имеем случайную (необученную) нейронную сеть, которая может по входному вектору input выдать случайный ответ, однако нам требуется ответы, удовлетворяющие конкретной задаче. Чтобы добиться этого нашу сеть необходимо обучить. Для этого нам необходима база тренировочных примеров, то есть множество пар векторов X - Y, на которых будет обучаться сеть. Обучать нейросеть мы будем с помощью алгоритма обратного распространения ошибки. Если кратко, то он работает следующим образом:
- Подать на вход сети обучающий пример (один входной вектор)
- Распространить сигнал по сети вперёд (получить выход сети)
- Вычислить ошибку (разница получившегося и ожидаемого векторов)
- Распространить ошибку на предыдущие слои
- Обновить весовые коэффициенты для уменьшения ошибки
Сам же алгоритм обучения выглядит так:
error = 0 epoch = 1 повторять: Для каждого обучающего примера: Найти ошибку e = f - d Прибавить к error сумму квадратов значений e Распространенить ошибку к первому слою Обновить веса если error < eps выйти если epoch > maxEpoch выйти из-за ограничения на число эпох epoch = epoch + 1
Обучаем нейронную сеть
Для обратного распространения ошибки нам потребуется знать значения входов, выходов и значения производных функции активации сети на каждом из слоёв, поэтому создадим структуру LayerT, в которой будет 3 вектора: x — вход слоя, z — выход слоя, df — производная функции активации. Также для каждого слоя потребуются векторы дельт, поэтому добавим в наш класс ещё и их. С учётом вышесказанного наш класс станет выглядеть так:
class Network {
struct LayerT {
public Vector x; // вход слоя
public Vector z; // активированный выход слоя
public Vector df; // производная функции активации слоя
}
Matrix[] weights; // матрицы весов слоя
LayerT[] L; // значения на каждом слое
Vector[] deltas; // дельты ошибки на каждом слое
int layersN; // число слоёв
public Network(int[] sizes) {
Random random = new Random(DateTime.Now.Millisecond); // создаём генератор случайных чисел
layersN = sizes.Length - 1; // запоминаем число слоёв
weights = new Matrix[layersN]; // создаём массив матриц весовых коэффициентов
L = new LayerT[layersN]; // создаём массив значений на каждом слое
deltas = new Vector[layersN]; // создаём массив для дельт
for (int k = 1; k < sizes.Length; k++) {
weights[k - 1] = new Matrix(sizes[k], sizes[k - 1], random); // создаём матрицу весовых коэффициентов
L[k - 1].x = new Vector(sizes[k - 1]); // создаём вектор для входа слоя
L[k - 1].z = new Vector(sizes[k]); // создаём вектор для выхода слоя
L[k - 1].df = new Vector(sizes[k]); // создаём вектор для производной слоя
deltas[k - 1] = new Vector(sizes[k]); // создаём вектор для дельт
}
}
// прямое распространение
public Vector Forward(Vector input) {
for (int k = 0; k < layersN; k++) {
if (k == 0) {
for (int i = 0; i < input.n; i++)
L[k].x[i] = input[i];
}
else {
for (int i = 0; i < L[k - 1].z.n; i++)
L[k].x[i] = L[k - 1].z[i];
}
for (int i = 0; i < weights[k].n; i++) {
double y = 0;
for (int j = 0; j < weights[k].m; j++)
y += weights[k][i, j] * L[k].x[j];
// активация с помощью сигмоидальной функции
L[k].z[i] = 1 / (1 + Math.Exp(-y));
L[k].df[i] = L[k].z[i] * (1 - L[k].z[i]);
// активация с помощью гиперболического тангенса
//L[k].z[i] = Math.Tanh(y);
//L[k].df[i] = 1 - L[k].z[i] * L[k].z[i];
// активация с помощью ReLU
//L[k].z[i] = y > 0 ? y : 0;
//L[k].df[i] = y > 0 ? 1 : 0;
}
}
return L[layersN - 1].z; // возвращаем результат
}
}
Обратное распространение ошибки
Перейдём к обратному распространению ошибки. В качестве функции оценки сети E(W) возьмём среднее квадратичное отклонение: E = 0.5 · Σ(y1i - y2i)2. Чтобы найти значение ошибки E, нам нужно найти сумму квадратов разности значений вектора, который выдала сеть в качестве ответа, и вектора, который мы ожидаем увидеть при обучении. Также нам потребуется найти дельту для каждого слоя, причём для последнего слоя она будет равна вектору разности полученного и ожидаемого векторов, умноженному (покомпонентно) на вектор значений производных последнего слоя: δlast = (zlast - d)·f'last, где zlast — выход последнего слоя сети, d — ожидаемый вектор сети, f'last — вектор значений производной функции активации последнего слоя.
Теперь, зная дельту последнего слоя, мы можем найти дельты всех предыдущих слоёв. Для этого нужно умножить транспонированную матрицы текущего слоя на дельту текущего слоя и затем умножить полученный вектор на вектор производных функции активации предыдущего слоя: δk-1 = WTk·δk·f'k.
Что ж, давайте реализуем это в коде:
// обратное распространение
void Backward(Vector output, ref double error) {
int last = layersN - 1;
error = 0; // обнуляем ошибку
for (int i = 0; i < output.n; i++) {
double e = L[last].z[i] - output[i]; // находим разность значений векторов
deltas[last][i] = e * L[last].df[i]; // запоминаем дельту
error += e * e / 2; // прибавляем к ошибке половину квадрата значения
}
// вычисляем каждую предудущю дельту на основе текущей с помощью умножения на транспонированную матрицу
for (int k = last; k > 0; k--) {
for (int i = 0; i < weights[k].m; i++) {
deltas[k - 1][i] = 0;
for (int j = 0; j < weights[k].n; j++)
deltas[k - 1][i] += weights[k][j, i] * deltas[k][j];
deltas[k - 1][i] *= L[k - 1].df[i]; // умножаем получаемое значение на производную предыдущего слоя
}
}
}
Изменение весов
Для того, чтобы уменьшить ошибку сети нужно изменить весовые коэффициенты каждого слоя. Как же именно нужно менять весовые коэффициенты матриц на каждом слое? Оказывается, всё довольно просто. Для этого используется метод градиентного спуска, а значит нам необходимо вычислить градиент по весам и сделать шаг в отрицательную сторону от этого градиента. На этапе прямого распространения мы зачем-то запоминали входные сигналы, а при обратном распространении ошибки мы вычисляли дельты в каждом слое. Именно их мы и будем сейчас использовать для нахождения градиента! Градиент по весам равен перемножению входного вектора и вектора дельт (не покомпонентно). Поэтому, чтобы обновить весовые коэффициенты и уменьшить тем самым ошибку сети нужно всего лишь вычесть из матрицы весов результат перемножения дельт и входных векторов, умноженный на скорость обучения. Это можно записать в таком виде: Wt+1 = Wt - η·δ·X, где Wt+1 — новая матрица весов, Wt — текущая матрица весов, X — входное значение слоя, δ — дельта этого слоя. Почему именно так с математической точки зрения хорошо описано в этой статье.
// обновление весовых коэффициентов, alpha - скорость обучения
void UpdateWeights(double alpha) {
for (int k = 0; k < layersN; k++) {
for (int i = 0; i < weights[k].n; i++) {
for (int j = 0; j < weights[k].m; j++) {
weights[k][i, j] -= alpha * deltas[k][i] * L[k].x[j];
}
}
}
}
Обучение сети
Теперь, имея методы прямого распространения сигнала, обратного распространения ошибки и изменения весовых коэффициентов, нам остаётся лишь соединить всё вместе в один метод обучения.
public void Train(Vector[] X, Vector[] Y, double alpha, double eps, int epochs) {
int epoch = 1; // номер эпохи
double error; // ошибка эпохи
do {
error = 0; // обнуляем ошибку
// проходимся по всем элементам обучающего множества
for (int i = 0; i < X.Length; i++) {
Forward(X[i]); // прямое распространение сигнала
Backward(Y[i], ref error); // обратное распространение ошибки
UpdateWeights(alpha); // обновление весовых коэффициентов
}
Console.WriteLine("epoch: {0}, error: {1}", epoch, error); // выводим в консоль номер эпохи и величину ошибку
epoch++; // увеличиваем номер эпохи
} while (epoch <= epochs && error > eps);
}
Сеть готова. Давайте же её чему-нибудь научим!
Тренируем нейросеть на функции XOR
Почему функция XOR так интересна? Просто потому, что её невозможно получить одним нейроном: 0 ^ 0 = 0, 0 ^ 1 = 1, 1 ^ 0 = 1, 1 ^ 1 = 0. Однако она легко получается увеличением числа нейронов. Мы же попробуем выполнить обучение сети с 3 нейронами в скрытом слое и 1 выходным (так как выход у нас всего один). Для этого нам необходимо создать массив векторов X и Y с обучающими данными и саму нейросеть:
// массив входных обучающих векторов
Vector[] X = {
new Vector(0, 0),
new Vector(0, 1),
new Vector(1, 0),
new Vector(1, 1)
};
// массив выходных обучающих векторов
Vector[] Y = {
new Vector(0.0), // 0 ^ 0 = 0
new Vector(1.0), // 0 ^ 1 = 1
new Vector(1.0), // 1 ^ 0 = 1
new Vector(0.0) // 1 ^ 1 = 0
};
Network network = new Network(new int[]{2, 3, 1}); // создаём сеть с двумя входами, тремя нейронами в скрытом слое и одним выходом
После чего запустим обучение со следующими параметрами: скорость обучения - 0.5, число эпох - 100000, величина ошибки - 1e-7:
network.Train(X, Y, 0.5, 1e-7, 100000); // запускаем обучение сети
После обучения посмотрим на результаты выполнив прямой проход для всех элементов:
for (int i = 0; i < 4; i++) {
Vector output = network.Forward(X[i]);
Console.WriteLine("X: {0} {1}, Y: {2}, output: {3}", X[i][0], X[i][1], Y[i][0], output[0]);
}
В результате вывод может быть таким:
X: 0 0, Y: 0, output: 0,00503439463431083 X: 0 1, Y: 1, output: 0,996036009216668 X: 1 0, Y: 1, output: 0,996036033202241 X: 1 1, Y: 0, output: 0,00550270947767007
Проверять результаты на тренировочной же выборке довольно скучно, ведь как никак на ней мы сеть обучали, но, увы, для XOR проблемы ничего другого не остаётся. В качестве более серьёзного примера рекомендуем выполнить задачу распознавания картинок с рукописными цифрами MNIST. Это база содержит 60000 картинок написанных от руки цифр размером 28 на 28 пикселей и используется как один из основных датасетов для начала изучения машинного обучения. Не смотря на простоту нашей сети, при грамотном выборе параметров (число нейронов, число слоёв, скорость обучения, число эпох...) можно получить точность распознавания до 98%! Проверить свою сеть вы можете, поучаствовав в соревновании на сайте Kaggle. Нашей команде удалось достичь точности в 98.171%! А вы сможете больше? :)
В заключение
Мы написали с вами нейронную сеть прямого распространения и даже обучили её функции XOR. При этом мы позаботились об универсальности, благодаря чему нейросеть может быть обучена на любых данных, главное только подготовить два массива обучающих векторов X и Y, подобрать параметры обучения и запустить само обучение, после чего наблюдать за процессом. Важно помнить, что при использовании сигмоидальной функции активации, выходные значения сети не будут превышать 1, а значит, для обучения данным, которые значительно больше 1 необходимо отнормировать их, то есть привести к отрезку [0, 1].
Возможно, будет интересно: Свёрточная нейронная сеть с нуля. Часть 0. Введение.